Bulldozer00's Blog

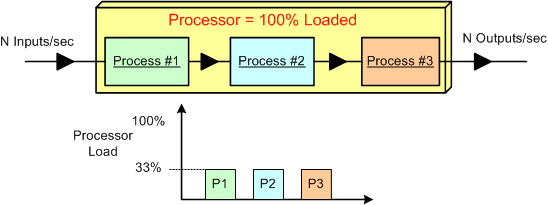
Assume that we have a data-centric, real-time product that: sucks in N raw samples/sec, does some fancy proprietary processing on the input stream, and outputs N value-added measurements/sec. Also assume that for N, the processor is 100% loaded and the load is equally consumed (33.3%) by three interconnected pipeline processes that crunch the data stream.

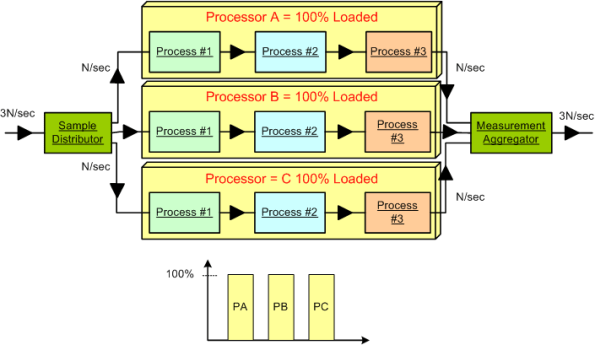
Next, assume that a new, emerging market demands a system that can handle 3*N input samples per second. The obvious solution is to employ a processor that is 3 times as fast as the legacy processor. Alternatively, (if the nature of the application allows it to be done) the input data stream can be split into thirds , the pipeline can be cloned into three parallel channels allocated to 3 processors, and the output streams can be aggregated together before final output. Both the distributor and the aggregator can be allocated to a fourth system processor or their own processors. The hardware costs would roughly quadruple, the system configuration and control logic would increase in complexity, but the product would theoretically solve the market’s problem and produce a new revenue stream for the org. Instead of four separate processor boxes, a single multi-core (>= 4 CPUs) box may do the trick.

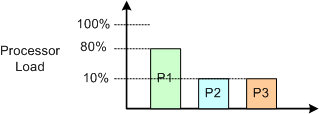
We’re not done yet. Now assume that in the current system, process #1 consumes 80% of the processor load and, because of input sample interdependence, the input stream cannot be split into 3 parallel streams. D’oh! What do we do now?

One approach is to dive into the algorithmic details of the P1 CPU hog and explore parallelization options for the beast. Assume that we are lucky and we discover that we are able to divide and conquer the P1 oinker into 5 equi-hungry sub-algorithms as shown below. In this case, assuming that we can allocate each process to its own CPU (multi-core or separate boxes), then we may be done solving the problem at the application layer. No?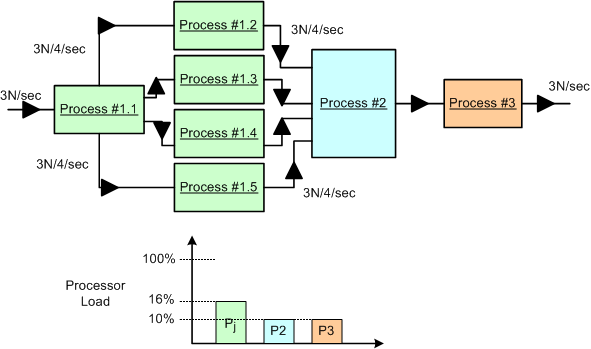

Do you detect any major conceptual holes in this blarticle?